1부 7장
7장 앙상블 학습과 랜덤 포레스트
- 7.1 투표 기반 분류기
- 7.2 배깅과 페이스팅
- 7.3 랜덤 패치와 랜덤 서브스페이스
- 7.4 랜덤 포레스트
- 7.5 부스팅
- 7.6 스태킹
뭔지 모르고 썼지만 성능이 좋았던 앙상블 기법... 오늘 한번 자세히 알아보도록 하자!!!
일단 먼저 앙상블 학습이 뭔지부터 알아야겠지?
앙상블 학습이란 여러 개의 예측 모델(예: 회귀, 분류 모델)을 결합하여 더 나은 결과를 얻는 기법으로, 다양한 알고리즘을 결합하여 사용하는 방식을 의미한다.
또한 오늘 중요하게 다룰 랜덤 포레스트는 이름에서 알 수 있겠지만
앙상블 학습 방법의 일종으로, 여러 개의 결정 트리를 사용하여 예측을 수행하며, 개별 트리의 예측을 결합하여 최종 예측을 만드는 것으로, 랜덤 포레스트는 오늘날 강력한 머신러닝 알고리즘으로 알려져 있다고 한다. (강력한!!)
07_ensemble_learning_and_random_forests.ipynb
Run, share, and edit Python notebooks
colab.research.google.com
여기 있는 코드들은 전부 위를 참고했다.
7.1 투표 기반 분류기
투표 기반 분류기는 앙상블 학습의 한 방식으로 여러 개의 개별 모델을 결합하여 더 높은 예측 성능을 달성하는 방법을 말한다.
개별 모델들이 약한 학습기라도 서로 결합하면 강한 학습기로서 더 나은 성능을 발휘할 수 있게된다.
이게 어떤 말인가라면 아래를 참고해보자.
- 개별 모델들이 정확도가 낮은 약한 학습기라도, 여러 개의 약한 학습기를 결합하면 강한 학습기가 된다. 예를 들어, 정확도가 51%에 불과한 분류기를 여러 개 결합하면 예측 성능이 향상된다.
- 이제 동일한 51% 정확도를 가진 분류기들을 1,000개 결합하여 다수결 원칙으로 예측을 수행한다고 가정해보자. 1,000개의 분류기가 각각 51%의 확률로 올바른 예측을 한다면, 이 1,000개 중 절반 이상(501개 이상)이 올바른 예측을 할 확률이 매우 높아진다.
- 1,000개의 분류기 중 과반수(501개 이상)가 올바르게 예측할 확률은 개별 분류기의 정확도가 50%보다 조금이라도 높다면, 즉 51%라면, 큰 수의 법칙에 의해 다수결 결과가 올바른 예측에 수렴할 가능성이 매우 높아지는데, 이는 각 분류기의 예측이 독립적이기 때문에 가능한 현상이라고 한다.
사이킷런은 이름/예측기 쌍의 리스트를 제공하기만 하면 일반 분류기처럼 쉽게 사용할 수 있는 VotingClassifier 클래스를 제공한다. 아래는 moons 데이터셋을 사용하는 예시이다.
from sklearn.datasets import make_moons
from sklearn.ensemble import RandomForestClassifier, VotingClassifier
from sklearn.linear_model import LogisticRegression
from sklearn.model_selection import train_test_split
from sklearn.svm import SVC
X, y = make_moons(n_samples=500, noise=0.30, random_state=42)
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=42)
voting_clf = VotingClassifier(
estimators=[
('lr', LogisticRegression(random_state=42)),
('rf', RandomForestClassifier(random_state=42)),
('svc', SVC(random_state=42))
]
)
voting_clf.fit(X_train, y_train)위의 코드는 moons 데이터셋을 로드하고 훈련 세트와 테스트 세트로 분할한 다음 세 가지 다양한 분류기로 구성된 투표 기반 분류기를 생성하고 훈련한다.
여기서 VotingClassifier를 훈련할 때, 이 클래스는 모든 추정기(개별 모델)를 복제하여 복제된 추정기를 학습시킨다. 원본 추정기는 estimators 속성을 통해 참조할 수 있으며, 훈련된 복제본은 estimators_ 속성에 저장되게 된다.
여기서 원본 추정기란, VotingClassifier에 입력으로 전달한 개별 분류기 객체들을 의미한다. 예를 들어, VotingClassifier를 구성할 때 로지스틱 회귀, 랜덤 포레스트, SVM 등 여러 분류기를 전달할 수 있는데, 이때 전달된 개별 분류기들이 원본 추정기이고 위의 코드에서는
('lr', LogisticRegression(random_state=42)),
('rf', RandomForestClassifier(random_state=42)),
('svc', SVC(random_state=42))
부분이 원본 추정기이다.
근데 왜 복제본을 만드는 걸까?
원본 모델을 유지하면서 앙상블 모델의 독립성 보장
- VotingClassifier는 다양한 분류기를 결합하여 앙상블 모델을 만드는데, 각 모델의 독립성이 중요하다. 그런데 만약 원본 모델 자체를 학습시켜버린다면, 원본 모델이 변형되어 이후 다른 곳에서 사용할 수 없게 될 것이다.
- 원본 모델을 그대로 두고 복제본을 만들어 학습시키면, 원본 모델은 영향을 받지 않고, VotingClassifier 내부에서만 훈련된 복제본을 사용하게 된다. 즉, 원본 모델을 유지하면서 앙상블 학습을 수행할 수 있는 것이니 얼마나 좋은가..!
for name, clf in voting_clf.named_estimators_.items():
print(name, "=", clf.score(X_test, y_test))
리스트 대신 덕셔너리를 전달히는 경우 named_estimators 또는 named_estimators_ 를 사용할 수 있다
voting_clf.predict(X_test[:1])
투표 기반 분류기의 predict() 메서드를 호출하면 직접 투표를 수행한다. 직접 투표는 아래에서 설명하도록 하겠다.
voting_clf.score(X_test, y_test)
투표 기반 분류기의 성능을 살펴보면 0.912로 lr, rf, svc보다 조금 높은 것을 확인할 수 있다!
투표 기반 분류기는 두 가지로 나눌 수 있다.
1. 직접 투표 (Hard Voting)
2. 간접 투표 (Soft Voting)
두 가지이다.
직접 투표 방식 (Hard Voting)
직접 투표 방식은 다수결 원칙을 기반으로 한다. 각 분류기가 독립적으로 예측을 수행하고, 가장 많이 선택된 클래스를 최종 예측으로 결정하게 된다.
직접 투표의 예시
예를 들어, 테스트 샘플 하나에 대해 다음과 같은 예측을 했다고 가정할 때,
- 로지스틱 회귀: 클래스 1 예측
- 랜덤 포레스트: 클래스 1 예측
- SVM: 클래스 0 예측
이 경우, 두 개의 분류기가 클래스 1을 선택했으므로, 최종 예측은 클래스 1이 되는 것!
간접 투표 방식 (Soft Voting)

여기서 각 모델이 예측한 확률을 보면,
- 로지스틱 회귀 : 이 데이터가 클래스 A일 가능성 60%
- 랜덤 포레스트 :클래스 A일 가능성 55%
- SVM : 클래스 A일 가능성 70%
간접 투표 방식에서는 각 모델의 확률을 평균 내어 최종적으로 가장 높은 확률을 가진 클래스를 선택해야 한다.
- 클래스 A에 대한 평균 확률: ( 0.60+0.55+0.70) /3 =
- 클래스 B에 대한 평균 확률: (0.40+0.45+0.30) /3 =
이제 클래스 A와 클래스 B의 평균 확률을 비교해 보면,
- 클래스 A의 평균 확률이 더 높으므로, 최종 예측은 클래스 A가 된다..!
간접 투표 방식을 쓰려면 필요한 조건
이 방식을 사용하려면 모델이 클래스의 확률을 계산할 수 있어야 한다. 로지스틱 회귀나 랜덤 포레스트 같은 모델은 기본적으로 확률을 계산할 수 있지만, SVM은 기본 설정으로는 불가능하기 때문에 SVM에서 확률을 사용하려면 probability=True로 설정해줘야 한다고 한다..
7.2 배깅과 페이스팅
다양한 분류기를 만드는 한 가지 방법은 각기 다른 훈련 알고리즘을 사용하는 것이다. 또 다른 방법은 같은 알고리즘을 사용하고 훈련 세트의 서브셋을 랜덤으로 구성하여 분류기를 각기 다르게 학습시키는 것이 있다. 이 때 샘플링 하는 방식에따라 두가지로 나눈다.
- 배깅(Bagging):
- 부트스트래핑(bootstrap aggregating)의 줄임말로, 훈련 데이터에서 중복을 허용하여 랜덤하게 샘플을 추출해 각 모델을 학습시키는 방법이다.
- 중복을 허용하기 때문에 동일한 데이터가 여러 모델에서 중복으로 학습될 수 있음.
- 페이스팅(Pasting):
- 배깅과 유사하지만 중복을 허용하지 않고 샘플링하여 모델을 학습시킨다.
- 데이터 중복이 없어 배깅과는 다른 학습 샘플 구성이 이루어짐.
여기서 샘플을 추출한다는 것은 (with GPT)
훈련 데이터셋이 [A, B, C, D, E]라는 5개의 데이터로 구성되어 있다고 가정해봅시다. 부트스트래핑을 사용하여 중복을 허용해 이 데이터셋에서 일부 샘플을 뽑아 각 모델을 학습시킬 수 있습니다. 예를 들어, 모델을 학습시키기 위해 랜덤하게 5개의 샘플을 뽑으면, 다음과 같은 샘플링이 가능해집니다:
- 첫 번째 샘플링 결과: [A, C, C, E, D]
- 두 번째 샘플링 결과: [B, B, D, A, E]
- 세 번째 샘플링 결과: [A, A, C, D, E]
이처럼 배깅의 경우 중복을 허용하기 때문에 같은 데이터가 여러 번 선택될 수 있게된다.
모든 예측기가 훈련을 마치면 앙상블은 예측을 만든다. 이 때
- 여러 모델이 각각 예측을 수행한 후, 그 결과를 결합하여 최종 예측을 생성한다.
- 분류 문제에서는 통계적 최빈값(가장 많이 예측된 결과)을 사용해 최종 예측을 결정하고, 회귀 문제에서는 평균을 계산하여 최종 예측을 만든다.
- 개별 예측기의 경우 크게 편향되어 있지만 집계 함수를 통해 편향과 분산을 모두 줄일 수 있다고 한다.
집계 함수가 뭔가 했더니 앙상블 학습에서 여러 모델의 예측 결과를 하나의 최종 예측 값으로 결합하는 함수를 의미했다.
집계 함수의 예시
- 분류 문제:
- 최빈값 (Mode): 개별 모델들이 예측한 클래스 중에서 가장 많이 예측된 클래스를 최종 예측으로 선택합니다. 예를 들어, 5개의 모델 중 3개가 클래스 A를 예측하고 2개가 클래스 B를 예측하면, 최종 예측은 클래스 A가 됩니다. 이를 다수결 투표 방식이라고도 합니다.
- 회귀 문제:
- 평균 (Mean): 개별 모델들이 예측한 값의 평균을 계산하여 최종 예측으로 사용합니다. 예를 들어, 5개의 모델이 각각 10, 12, 11, 13, 12를 예측했다면, 이 값들의 평균인 11.6이 최종 예측이 됩니다.
결국 위에서 다 한말이었네... 책이 살짝 불친절 한듯. 아닌가 내가 잘 이해를 못하는 건가?
7.2.1 사이킷런의 배깅과 페이스팅
사이킷런에서 BaggingClassifier를 사용하여 간단하게 배깅 또는 페이스팅을 구현할 수 있다.
아래는 결정 트리 분류기로 500개의 앙상블을 훈련시키는 코드이다.
from sklearn.ensemble import BaggingClassifier
from sklearn.tree import DecisionTreeClassifier
bag_clf = BaggingClassifier(DecisionTreeClassifier(), n_estimators=500,
max_samples=100, n_jobs=-1, random_state=42)
bag_clf.fit(X_train, y_train)
여기서 bootstrap=True로 설정하면 배깅을 사용하고, bootstrap=False로 설정하면 페이스팅을 사용할 수 있으니 참고하자.
아무것도 쓰지 않으면 기본값은 bootstrap=True이므로 위는 배깅을 사용한 코드이다.

위의 사진은 결정 트리와 배깅을 사용한 결정 트리인데 배깅을 사용한 결정 트리가 훨씬 일반화가 잘된 것을 확인할 수 있다.
- 단일 결정 트리는 특정 데이터에 과적합될 가능성이 크지만, 배깅 앙상블은 여러 트리를 통해 예측을 결합하여 더 일반화된 경계선을 형성한다고 한다.
- 배깅은 각 예측기가 학습하는 데이터에 다양성을 추가하므로, 페이스팅보다 편향이 조금 더 높을 수 있지만, 분산이 줄어들어 일반적으로 더 나은 예측 성능을 보인다고 한다.
(성능충...)
단일 결정 트리 예시
단일 결정 트리는 전체 100명의 데이터를 사용해 하나의 결정 트리를 학습합니다. 이 트리는 데이터를 세밀하게 학습해 높은 훈련 정확도를 보일 수 있지만, 테스트 데이터에는 과적합될 가능성이 큽니다.
- 예를 들어, 훈련 데이터를 바탕으로 다음과 같이 예측한다고 해봅시다:
- 공부 시간이 1시간이면 시험 점수는 50점 예측
- 공부 시간이 2시간이면 시험 점수는 60점 예측
- 공부 시간이 3시간이면 시험 점수는 70점 예측
- 공부 시간이 4시간이면 시험 점수는 85점 예측
- 공부 시간이 5시간이면 시험 점수는 90점 예측
배깅을 사용한 결정 트리 예시
배깅은 100명의 학생 데이터를 중복을 허용하여 여러 샘플로 나누고, 각각의 샘플에 대해 여러 개의 결정 트리를 학습시킵니다. 각 트리는 일부 데이터만 학습하므로, 조금씩 다른 규칙을 학습하게 됩니다.
- 예를 들어, 100명의 학생 데이터에서 일부를 중복 포함하여 80명의 데이터로 첫 번째 결정 트리를 학습합니다.
- 공부 시간이 1시간이면 52점 예측
- 공부 시간이 2시간이면 62점 예측
- 공부 시간이 3시간이면 72점 예측
- 공부 시간이 4시간이면 80점 예측
- 공부 시간이 5시간이면 88점 예측
- 또 다른 트리는 다른 80명의 데이터로 학습하여 조금 다른 예측을 하게 됩니다.
- 공부 시간이 1시간이면 48점 예측
- 공부 시간이 2시간이면 58점 예측
- 공부 시간이 3시간이면 70점 예측
- 공부 시간이 4시간이면 82점 예측
- 공부 시간이 5시간이면 91점 예측
- 이런 식으로 10개의 결정 트리를 학습시키면, 각 트리가 조금씩 다른 규칙을 가지게 되며, 각 트리의 예측을 결합하여 최종 예측을 만듭니다.
7.2.2 OOB 평가
OOB 샘플:
- 배깅(Bagging)에서는 일부 데이터를 중복 허용하여 샘플링하는데, 이 과정에서 선택되지 않은 데이터가 발생한다. 이를 OOB 샘플(Out-Of-Bag Sample)이라고 부른다.
- 평균적으로, 훈련 데이터의 약 63%가 샘플링되고 나머지 37%가 OOB 샘플로 남는다고 한다.
- 이때 OOB 샘플은 각 개별 모델에 대해 학습에 사용되지 않았으므로 별도의 검증 세트 없이도 모델 성능을 평가할 수 있는 역할을 하게 된다.
- oob_score=True로 설정하면 사이킷런의 BaggingClassifier에서 자동으로 OOB 평가를 수행한다.
bag_clf = BaggingClassifier(DecisionTreeClassifier(), n_estimators=500,
oob_score=True, n_jobs=-1, random_state=42)
bag_clf.fit(X_train, y_train)
bag_clf.oob_score_
OOB 평가 결과를 보면 BaggingClassifier는 테스트 세트에서 약 89.6%의 정확도를 얻을 것으로 보인다.
from sklearn.metrics import accuracy_score
y_pred = bag_clf.predict(X_test)
accuracy_score(y_test, y_pred)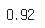
테스트 셋에서는 92%의 정확도를 얻었다 한 2%정도 차이난다...
첨에는 OOB가 뭔지 잘 이해가 안됐는데, train_test_split가 생각났다. 주로 훈련셋에서 모델 검증을 위해서 저걸로 나눴던 것이 기억나는데 OOB는 저기서 37%로 나눈 검증 세트 역할을 하면 된다고 생각하면 쉽다.
7.3 랜덤 패치와 랜덤 서브스페이스
- BaggingClassifier는 max_samples와 max_features를 이용하여 샘플링된 데이터와 특징을 선택하는 방식을 조절할 수 있다.
- 랜덤 패치 방식 (Random Patches Method) 훈련 샘플과 특징을 모두 샘플링하여 사용하는 방식이다. 예를 들어, max_samples=0.5와 max_features=0.5로 설정하면 훈련 샘플과 특징의 각각 50%만 랜덤하게 사용할 수 있다.
- 랜덤 서브스페이스 방식 (Random Subspaces Method) 모든 훈련 샘플을 사용하되, 일부 특징만을 샘플링해 사용하는 방식이다. bootstrap_features=True와 max_features를 설정하여 특징을 무작위로 선택한다. 이 방법은 주로 편향을 줄이는 대신 분산을 낮추기 위한 용도로 사용한다고 한다.

7.4 랜덤 포레스트
- 랜덤 포레스트는 배깅 방식을 적용한 다수의 결정 트리로 구성된 앙상블 학습 모델로, RandomForestClassifier를 사용해 손쉽게 구현할 수 있다.
아래는 랜덤 포레스트 분류기를 가능한 모든 CPU 코어에서 훈련시키는 코드이다.
from sklearn.ensemble import RandomForestClassifier
rnd_clf = RandomForestClassifier(n_estimators=500, max_leaf_nodes=16,
n_jobs=-1, random_state=42)
rnd_clf.fit(X_train, y_train)
y_pred_rf = rnd_clf.predict(X_test)- 랜덤 포레스트의 특징
- 각 트리의 노드를 분할할 때 전체 특징이 아닌 무작위로 선택된 특징 중 최적의 분할을 찾습니다.
- 기본적으로 $\sqrt{n}$ 개의 특징을 사용하며, 이는 트리의 다양성을 증가시켜 편향에서 손해보는 대신 과적합을 방지하고 분산을 줄이는 효과가 있다고 한다.
7.4.1 엑스트라 트리
- 엑스트라 트리는 일반적인 랜덤 포레스트와 달리 노드 분할 시 특징의 최적 임곗값을 찾는 대신, 임곗값을 무작위로 선택하여 분할을 수행한다.
- 이 방식은 트리를 더욱 랜덤하게 만들며, 특히 계산 시간이 줄어들어 훈련 속도가 빨라진다.
- 그러나 임곗값을 최적화하지 않기 때문에, 일반적으로 편향이 증가하고 분산이 줄어드는 효과가 있다.
반면에
- 엑스트라 트리는 ExtraTreesClassifier 또는 ExtraTreesRegressor 클래스를 사용하여 구현한다.
- RandomForestClassifier와 비슷한 사용법을 가지며, 기본적으로 bootstrap=False로 설정되어 있다고 한다.
- 이 모델은 RandomForestClassifier와 비교해 성능 차이가 크게 나지 않으며, 때로는 더 좋은 성능을 보이기도 하기 때문에 RandomForestClassifier와 ExtraTreesClassifier 둘다 사용해 보는 것이 좋다고 한다.
예시 (with GPT)
- 랜덤 포레스트는 길을 찾기 위해 지도를 열심히 보면서 가장 빠른 길을 찾아가려는 사람과 같습니다. 지도를 보고 분석하는 시간이 필요하지만, 더 빠르고 정확하게 목적지에 도착할 가능성이 높습니다.
- 엑스트라 트리는 지도를 보지 않고 무작위로 길을 선택해서 그냥 가보는 사람과 비슷합니다. 지도를 보며 최적의 길을 찾는 시간이 절약되지만, 목적지에 도착하는 길이 조금 비효율적일 수 있습니다. 대신, 빠르게 다양한 길을 시도할 수 있습니다.
7.4.2 특성 중요도
랜덤 포레스트는 여러 개의 결정 트리를 사용하여 예측을 수행하는데, 각 트리에서 어떤 특성을 사용하여 노드를 분할하는지에 따라 특성의 중요도를 계산할 수 있다.!!
그 전에 불순도에 대해 알아야 한다. (뭔가 배웠던 것 같은데)
- 불순도는 데이터가 얼마나 섞여 있는지를 측정하는 지표이다.
- 예를 들어, 분류 문제에서 한 노드에 다른 클래스(예: 개와 고양이)가 섞여 있다면 불순도가 높다고 할 수 있으며
- 반대로 한 노드에 같은 클래스(예: 개만)가 모여 있다면 불순도가 낮다고 할 수 있다.
- 따라서 불순도를 낮추는 것은 데이터를 잘 분류할 수 있다는 뜻이 된다.
불순도를 확인하면서 어떻게 측정하냐면 아래를 따른다.
특정 특성을 사용하여 노드를 분할할 때 불순도가 얼마나 줄어들었는지 확인
- 예를 들어, "꽃잎의 길이"라는 특성을 사용해서 데이터를 분할했더니 불순도가 크게 줄어들었다면, 이 특성은 데이터를 잘 구분하는 중요한 특성이라는 의미를 갖게 된다.
- 특성을 사용해 분할한 후, 평균적으로 불순도가 얼마나 줄어들었는지를 모든 트리에서 계산.
- 랜덤 포레스트는 여러 개의 결정 트리를 사용하므로, 모든 트리에서 해당 특성이 얼마나 불순도를 줄였는지 확인하고, 그 평균을 계산하여 계산을 한다.
- 불순도를 많이 줄여주는 특성일수록 중요도가 높아짐.
- 따라서 불순도를 크게 줄이는 특성일수록 모델에 더 중요한 특성으로 간주된다.
사이킷런에서 훈련이 끝난 뒤 특성마다 자동으로 이 점수를 계산하고 중요도의 전체 합이 1 이 되도록 결과값을 정규화한다.
이 값은 feature_importances_ 변수에 저장된다.
from sklearn.datasets import load_iris
iris = load_iris(as_frame=True)
rnd_clf = RandomForestClassifier(n_estimators=500, random_state=42)
rnd_clf.fit(iris.data, iris.target)
for score, name in zip(rnd_clf.feature_importances_, iris.data.columns):
print(round(score, 2), name)

위의 코드는 iris 데이터셋에 랜덤포레스트를 훈련시키고 각 특성의 중요도를 출력한 모습이다. 꽃잎의 길이(petal length)와 너비(petal width)가 중요한 것으로 나타난 것을 볼 수 있다!
7.5 부스팅
부스팅은 여러 개의 약한 학습기(정확도가 낮은 모델)를 연속적으로 학습시키고 결합하여 강한 학습기(높은 정확도의 모델)를 만드는 앙상블 학습 방법을 말한다. 앞의 모델이 틀린 부분을 보완해 나가는 방식을 기준으로 한다.
7.5.1 AdaBoost
이전 예측기를 보완하는 새로운 예측기를 만드는 방법은 이전 모델이 과소적합했던 훈련 샘플의 가중치를 더 높이는 것이다. 이렇게 하면 새로운 예측기는 학습하기 어려운 샘플에 점점 더 맞춰지게되는데 이것이 AdaBoost의 핵심 방식이다.
AdaBoost의 단계별 학습 과정 (with GPT)
- 초기 학습과 가중치 설정
- 첫 번째 학습기를 만들 때, 모든 샘플에 동일한 가중치를 부여합니다. 예를 들어, 샘플이 100개라면 각 샘플의 초기 가중치는 1/100입니다.
- 학습기가 처음으로 데이터를 학습하고, 예측을 수행합니다.
- 첫 번째 학습기의 오류 계산과 가중치 조정
- 첫 번째 학습기의 예측 결과에서 틀린 샘플을 식별하고, 이 샘플들의 가중치를 증가시킵니다.
- 틀린 예측에 대한 가중치를 높임으로써, 다음 학습기가 이 샘플들을 더 중요하게 학습하도록 유도합니다.
- 두 번째 학습기 학습과 반복적인 가중치 업데이트
- 두 번째 학습기는 첫 번째 학습기의 실수를 보완하도록, 가중치가 높아진 샘플에 더 중점을 두고 학습합니다.
- 두 번째 학습기 역시 예측을 수행하고, 틀린 샘플에 대한 가중치를 다시 조정합니다.
- 이러한 과정이 각 학습기마다 반복되면서, 모델이 점점 더 어려운 샘플을 맞추도록 개선됩니다.
- 최종 예측
- 모든 학습기가 학습을 마치면, 각 학습기의 예측 결과를 가중치를 반영하여 결합합니다.
- 정확도가 높은 학습기는 더 높은 가중치가 부여되고, 각 학습기의 예측을 종합하여 최종 결과를 예측합니다.

위 사진은 moons 데이터셋에 훈련시킨 다섯 개의 연속된 예측기의 결정 경계이다. 첫 번째 분류기가 많은 샘플을 잘못 분류해서 이 샘플들의 기중치가 높아졌고, 따라서 두 번째 분류기는 이 샘플들을 더 정확히 예측하게 된다.
오른쪽 그래프는 학습률을 반으로 낮춘 것만 빼고 똑같은 일련의 예측기를 나타낸 것이다.
- 학습률이 높을 때 (learning_rate = 1): 모델이 더 빠르게 적합되지만, 데이터에 지나치게 맞추려는 경향이 생길 수 있다. 또한 복잡한 결정 경계가 형성되며, 과적합의 위험이 크다는 단점이 있다.
- 학습률이 낮을 때 (learning_rate = 0.5): 모델이 천천히 적합되며, 결정 경계가 단순해진다. 이는 과적합을 줄이고 일반화 성능을 향상시키는 데 도움이 된다!
다음은 AdaBoost 알고리즘을 더 자세히 들여다 보는 과정이다.
1. 샘플의 초기 가중치 설정
모든 샘플 \( i \)에 대해 초기 가중치 \( w^{(1)}_i \)는 다음과 같다.
\[w^{(1)}_i = \frac{1}{m}\]
여기서 \( m \)은 샘플의 총 개수
2. 오류율 \(r_ 계산
\[r_j = \frac{\sum_{i=1}^m w_i^{(j)} \cdot \mathbb{I}(y_i \neq h_j(x_i))}{\sum_{i=1}^m w_i^{(j)}}\]
여기서:
- \( w_i^{(j)} \): 학습기 \( j \)에서 샘플 \( i \)의 가중치
- \( \mathbb{I}(y_i \neq h_j(x_i)) \): 샘플 \( i \)가 학습기 \( j \)에 의해 잘못 분류된 경우 \( 1 \), 그렇지 않으면 \( 0 \)을 반환하는 지시 함수
- \( y_i \): 샘플 \( i \)의 실제 레이블
- \( h_j(x_i) \): 학습기 \( j \)가 샘플 \( i \)에 대해 예측한 값
3. 학습기의 가중치 \( \alpha_j \) 계산
학습기 \( j \)의 가중치 \( \alpha_j \)는 다음과 같다.
\[
\alpha_j = \eta \cdot \log \left( \frac{1 - r_j}{r_j} \right)
\]
여기서:
- \( \eta \): 학습률, 기본값은 1
- \( r_j \): 학습기의 오류율
여기서 예측기가 정확할수록 가중치는 더 높아진다고 한다. 랜덤 추측이라면 가중치는 0에 가까워지는데 랜덤 추측보다 정확도가 낮으면 가중치는 음수가 될 수도 있다.
4. 샘플 가중치 업데이트
샘플 \( i \)의 가중치 업데이트 공식은 다음과 같다.
\[
w^{(j+1)}_i = w^{(j)}_i \cdot \exp \left( \alpha_j \cdot \mathbb{I}(y_i \neq h_j(x_i)) \right)
\]
여기서:
- \( w^{(j+1)}_i \): 업데이트된 가중치
- \( \exp(\alpha_j) \): 학습기의 가중치를 기반으로 잘못된 예측에 대해 가중치를 더 높이는 역할
- \( \mathbb{I}(y_i \neq h_j(x_i)) \): 잘못 분류된 경우 \( 1 \), 올바르게 분류된 경우 \( 0 \)
5. 가중치 정규화
모든 샘플의 가중치를 정규화하여 총합이 1이 되도록 한다.
\[
w^{(j+1)}_i = \frac{w^{(j+1)}_i}{\sum_{i=1}^m w^{(j+1)}_i}
\]
6. 최종 예측 (앙상블 예측)
모든 학습기의 예측을 종합하여 최종 예측을 다음과 같이 만든다.
\[
\hat{y}(x) = \arg\max_k \sum_{j=1}^N \alpha_j \cdot \mathbb{I}(h_j(x) = k)
\]
여기서:
- \( \hat{y}(x) \): 입력 \( x \)에 대한 최종 예측
- \( N \): 학습기의 총 개수
- \( h_j(x) \): 학습기 \( j \)가 \( x \)에 대해 예측한 클래스
- \( \alpha_j \): 학습기 \( j \)의 가중치
사이킷런에서는 AdaBosstClassifier를 사용하여 분류기를 훈련시킬 수 있다. 아래 코드 참고!
from sklearn.ensemble import AdaBoostClassifier
ada_clf = AdaBoostClassifier(
DecisionTreeClassifier(max_depth=1), n_estimators=30,
learning_rate=0.5, random_state=42)
ada_clf.fit(X_train, y_train)
7.5.2 그레이디언트 부스팅
- 그레디언트 부스팅은 순차적으로 약한 학습기를 추가하여 앙상블을 만드는 방법이다.
- AdaBoost처럼 반복마다 샘플의 가중치를 수정하는 대신에 각 학습기는 이전 예측기의 오류(잔여 오차, residual error)를 줄이는 데 중점을 두는 것이 핵심이다.
결정 트리를 기반 예측기로 사용하는 간단한 회귀 문제를 푸는 것을 그레이디언트 트리 부스팅(gradient tree boosting) 또는 그레이디언트 부스티드 회귀 트리(gradient boosted regression tree)라고 한다.
import numpy as np
from sklearn.tree import DecisionTreeRegressor
np.random.seed(42)
X = np.random.rand(100, 1) - 0.5
y = 3 * X[:, 0] ** 2 + 0.05 * np.random.randn(100) # y = 3x² + Gaussian noise
tree_reg1 = DecisionTreeRegressor(max_depth=2, random_state=42)
tree_reg1.fit(X, y)
위의 코드를 통해 간단한 2차방정식 데이터셋을 만들고 여기에 `DecisionTreeRegressor 를 훈련시켜 보자.
y2 = y - tree_reg1.predict(X)
tree_reg2 = DecisionTreeRegressor(max_depth=2, random_state=43)
tree_reg2.fit(X, y2)
y3 = y2 - tree_reg2.predict(X)
tree_reg3 = DecisionTreeRegressor(max_depth=2, random_state=44)
tree_reg3.fit(X, y3)
X_new = np.array([[-0.4], [0.], [0.5]])
sum(tree.predict(X_new) for tree in (tree_reg1, tree_reg2, tree_reg3))
사이킷런의 GradientBoostingRegressor를 사용하면 GBRT 앙상블을 간단하게 훈련시킬 수 있다 아래는 코드이다.
from sklearn.ensemble import GradientBoostingRegressor
gbrt = GradientBoostingRegressor(max_depth=2, n_estimators=3,
learning_rate=1.0, random_state=42)
gbrt.fit(X, y)
여기서 learning_rate는 학습률로 각 학습기의 기여도를 조절한다. 낮은 값을 설정하면 더 많은 학습기가 필요하지만 과적합 위험이 줄어든다. 이를 축소(shrinkage)라고 부르는 규제 방법중 하나라고 한다.

n_estimators: 앙상블에 포함될 학습기의 수로 왼쪽은 적은 트리의 개수, 오른쪽은 적절한 개수의 트리를 사용한 것으로 만약 너무 많은 학습기를 설정하면 과적합될 수 있다.
gbrt_best = GradientBoostingRegressor(
max_depth=2, learning_rate=0.05, n_estimators=500,
n_iter_no_change=10, random_state=42)
gbrt_best.fit(X, y)
이 때 적절한 트리의 개수를 찾기 위해서 n_iter_no_change 파라미터를 설정해주어야 한다. 모델 성능이 일정 횟수 동안 개선되지 않으면 훈련을 중단하는 방식이다. (earlystopping 인듯..?) 과적합을 방지하고 훈련 속도를 개선하는 데 도움을 준다고 한다..
근데 너무 높게하면 과적합 될 수도 있다고 하니 조심해서 잘 설정하자.
- n_iter_no_change를 설정하면 fit() 메소드가 검증 세트를 따로 분리하여 매 반복마다 성능을 확인하고, 추가적인 학습이 의미가 없다고 판단되면 멈추게 된다.
- 검증 세트의 크기는 validation_fraction 파라미터로 조정할 수 있으며, 기본값은 전체 데이터의 10%라고 한다.
- 또한, tol 파라미터를 통해 무시할 수 있는 성능 향상 허용치를 설정할 수 있다. 기본값은 0.0001
또한 subsample 매개변수도 지원한다.
- subsample: 이 파라미터는 각 트리가 학습할 때 사용할 샘플의 비율을 지정할 수 있다.
- subsample=0.25로 설정하면 각 트리는 랜덤하게 선택된 25%의 샘플만으로 학습하게 됨.
- 이렇게 하면 개별 트리가 학습하는 데이터가 다양해져 편향이 줄어들지만, 분산이 약간 높아질 수 있다. 즉, 모델이 좀 더 일반화된 예측을 하게 되는 효과가 있다.
- 또한, subsample을 낮게 설정하면 학습 속도가 빨라지는 장점이 있다. 이 방식을 확률적 그레디언트 부스팅이라고 부른다고 한다!!!
7.5.3 히스토그램 기반 그레이디언트 부스팅
히스토그램 기반 그레이디언트 부스팅(HGB)은 큰 데이터셋에 최적화된 새로운 GBRT 방식으로, 입력 특성을 구간으로 나누어 정수로 대체하는 방식의 알고리즘이다.
- 구간화 작업:
- HGB는 연속적인 데이터를 max_bins 하이퍼파라미터에 설정된 수만큼 구간으로 나누어 각 구간을 정수로 표현한다. 기본값은 255이고 더 높게 설정할 수는 없다고 한다.
- 이로 인해 각 트리 학습 시 특정 분할을 적용할 때 가능한 임계값 수를 줄여주어 학습 속도가 향상된다고 한다.
- 계산 복잡도 감소:
- 일반적인 그레이디언트 부스팅의 계산 복잡도는 샘플 개수와 특성 개수에 비례하여 증가하지만, HGB는 구간 개수와 특성 개수만을 고려하기 때문에 대규모 데이터에서도 빠르게 학습할 수 있게 된다!
- 하지만 구간 분할이 규제처럼 작동해 정밀도 손실을 유빌하므로 데이터셋에 따라 과대적합을 줄이는 데 도움이 될 수도 있고 과소적합을 유발할 수도 있다.
사이킷런에서 HGB 구현을 위해서는 HistGradientBoostingRegressor와 HistGradientBoostingClassifier 클래스를 사용하여 HGB를 간편하게 구현할 수 있다. GradientBoostingClassifier와 유사하지만 몇 가지 주목할 만한 차이점은
1. 인스턴스 수가 10000개보다 많으먼 조기 종료가 자동으로 활성화 됨.
2. n_estimators 매개변수 대신 max_iter로 반복 수를 제어
3. subsample 매개변수가 지원되지 않는 점등이 있다.
HGB 클래스는 범주형 특성과 누락된 값을 지원해서 전처리가 상당히 편하다!! (너무 좋아)
- 파이프라인을 사용하여 누락된 값을 채우거나 스케일 조정을 별도로 할 필요 없이 간단히 데이터셋을 처리할 수 있다
- 원-핫 인코딩과 같은 복잡한 인코딩을 하지 않고도 OrdinalEncoder를 통해 범주형 데이터를 효율적으로 다룰 수 있다.
7.6 스태킹
마지막 앙상블 모텔은 스태킹(stacking)이다. 스태킹은 여러 예측기의 출력을 결합하여 최종 예측을 만들어내는 앙상블 방법 중 하나이다. 하지만 단순히 각 예측기의 결과를 평균하거나 투표하는 대신, 블렌더(또는 메타 학습기)라는 모델을 학습시켜 예측기의 출력을 조합하는 방식이다.
스태킹의 주요 단계 (with GPT)
- 개별 예측기(기본 학습기) 훈련:
- 데이터셋을 사용하여 각 예측기(예: 로지스틱 회귀, 랜덤 포레스트, SVM 등)를 개별적으로 학습합니다.
- 각 예측기는 원본 훈련 데이터셋을 사용하여 독립적으로 예측을 수행합니다.
- 예를 들어, 세 가지 기본 학습기가 각각 학습을 통해 새로운 샘플에 대해 3.1, 2.7, 2.9라는 예측 결과를 생성합니다.
- 교차 검증을 통한 블렌더 훈련 데이터 생성:
- 교차 검증(cross_val_predict)을 사용하여 각 예측기가 훈련 셋에 대해 예측한 값을 생성합니다. 이때, 모델이 해당 샘플에 대해 이미 학습된 정보가 없는 상태에서 예측을 수행하여 과적합을 방지합니다.
- 교차 검증의 과정에서 얻은 예측값은 블렌더를 훈련하기 위한 새로운 특성으로 사용됩니다.
- 예를 들어, 원본 훈련 세트의 각 샘플에 대해, 예측기 1, 2, 3이 예측한 값이 각각 하나의 특성으로 추가되어 새로운 블렌딩 훈련 세트를 구성하게 됩니다.

- 블렌더 학습:
- 블렌더(메타 모델)는 교차 검증으로 생성된 예측값을 입력 데이터로 사용하여 학습을 진행합니다.
- 블렌더는 각 예측기 결과의 조합 방법을 학습하여, 개별 예측기의 약점을 보완하고 강점을 결합할 수 있도록 최종 예측을 수행할 방법을 찾습니다.
- 블렌더가 최종적으로 예측하는 값은 각 기본 학습기의 예측 결과에 기반하므로, 블렌더가 제대로 학습된다면 개별 예측기들보다 높은 성능을 낼 가능성이 큽니다.
- 테스트 셋 예측:
- 블렌더가 학습되면, 새로운 데이터에 대해 각 기본 학습기가 예측을 수행하고, 그 결과를 블렌더의 입력으로 사용하여 최종 예측을 도출합니다.
- 블렌더가 출력하는 최종 예측 값은 기본 학습기들의 예측을 조합한 결과입니다.
사이킷런에는 스태킹 앙상블을 위한 StackingClassifier와 StackingRegressor 클래스가 있다. 아래는 그 코드 이다.
from sklearn.ensemble import StackingClassifier
from sklearn.linear_model import LogisticRegression
from sklearn.ensemble import RandomForestClassifier
from sklearn.svm import SVC
stacking_clf = StackingClassifier(
estimators=[
('lr', LogisticRegression(random_state=42)),
('rf', RandomForestClassifier(random_state=42)),
('svc', SVC(probability=True, random_state=42))
],
final_estimator=RandomForestClassifier(random_state=43),
cv=5 # 교차 검증 폴드 개수
)
stacking_clf.fit(X_train, y_train)
'로봇 > 인공지능, AI' 카테고리의 다른 글
| [핸즈온 머신러닝 3판] 9.비지도 학습 (군집만) (2) | 2024.11.24 |
|---|---|
| [핸즈온 머신러닝 3판] 8.차원 축소 (1) | 2024.11.17 |
| [핸즈온 머신러닝 3판] 5.서포트 벡터 머신 (1) | 2024.11.03 |
| [핸즈온 머신러닝 3판] 6.결정 트리 (0) | 2024.10.26 |
| Gymnasium을 사용한 Double-inverted-pendulum (1) | 2024.10.12 |




